基本回路と特性
リプルフィルタは、ひとことでいえば、「直流」は流すが、「50Hz、60Hz、100Hzあるいは120Hz」の交流はカットしたい、という「ロー・パス・フィルター」です。基本回路は、下図のようになります。1kΩの抵抗と、47μFのコンデンサでロー・パス・フィルターを作ってみました。（注：本章では、50Hzの商用電源ということで計算しています）
図1
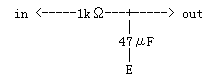
このフィルターがどのような特性であるのか、ちょっと調べてみたのが下図です。（注：「基準特性その１」にもとずく簡易計算です。また、out側のインピーダンスは考えないことにしています）
図2
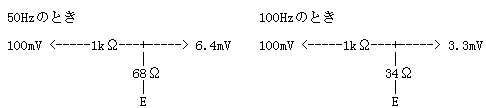
図3
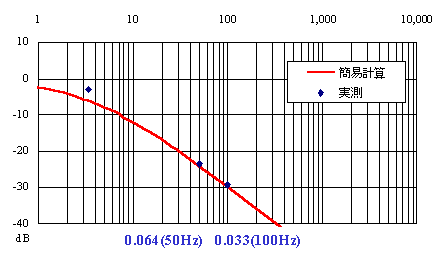
半波整流したときのリプルのときで0.064倍（-23.2dB）、両波整流したときのリプル（同100Hz）で0.033倍（-29.5dB）の減衰が得られるハイ・パス・フィルターです。もし、残留リプルが100mVあるところにこのフィルターを挿入してやると、残留リプルはそれぞれの場合で6.4mV、3.3mVまで少なくできるわけです。
リプル・フィルターの設計では、簡易計算のよるコンデンサのリアクタンスと抵抗値とで求めることができた減衰率をそのまま適用していいと思います。この計算方法で求めた残留リプルの値が、目標値よりも十分低くなってくれれば「よし」とします。
電圧降下とフィルタ段数
抵抗とコンデンサによるリプル・フィルターでは、必ず抵抗による直流電圧のロスが生じます。図1、図2のケースでは100Hzでのフィルタ効果は0.033倍でしたが、1kΩの抵抗があるために、もしここに10mAの電流が流れているとすると、10mA × 1kΩ＝10Vの電圧降下が生じます。回路の都合上、どうしても電圧降下を5Vにおさえたいが、0.033倍以上のフィルタ効果が欲しい場合はどうしたらいいでしょうか。抵抗は510Ωにせざるを得ません。このまま47μFのコンデンサを使うと、フィルタ効果は、34Ω /（34Ω＋510Ω）＝0.063倍と半減してしまいます。そこで、コンデンサ容量を100μFに増量してやります。すると、16Ω /（16Ω＋510Ω）＝0.0304倍となって目標値を達成できることがわかります。
もうひとつの方法は、フィルタの段数を増やすというものです。240Ωの抵抗2本と47μFのコンデンサ2個で2段フィルタとしたらどうでしょうか。
図4
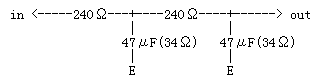
フィルタ効果を計算してみると、1段あたり、34Ω /（34Ω＋240Ω）＝0.124倍でこれが2段分ですから、0.124倍 × 0.124倍＝0.0154倍となります。このように、1段フィルタのままでコンデンサ容量を大きくするよりも、段数を増やす方がはるかに大きなフィルタ効果が得られます。(注：各段のフィルタはお互いに干渉し合うのでこの計算は正確ではありませんが、結論はかわりません。)
整流直後の残留リプル
さて、問題となるのは、整流直後の残留リプルがどれくらいあるのかということです。これがわからないと、いくらリプル・フィルターの特性を計算しても意味がありません。本来は、「電源の内部抵抗(Rs)」、「負荷抵抗(RL)」、「電源周波数」、「整流方式(全波か半波か)」、「平滑コンデンサ容量」これらから「整流出力電圧(Eo)」を求め、さらに「リプル含有率(%)」さらに「リプル電圧(Er)」を求めるというのが正しいお作法です。しかし、この方法で計算するには「ωRLCとRs/RL(%)からEo/E(rms)を求める図表」というのと「ωRLCと整流方式とRs/RL(%)からEr/Eo(%)を求める図表」という2つの厄介な図表と格闘しなければなりません。
本章では、もっと楽に残留リプルが求まる方法をご紹介しますが、どうしてもちゃんと計算したいという方は、トランジスタ技術 SPECIAL No.1特集「個別半導体素子活用法のすべて」ＣＱ出版社に掲載されていますから、チャレンジしてみてください。この本は、今でも大きな書店にゆけば入手可能ですし、半導体に関して非常に役に立つ情報が満載された本ですから、是非入手されることをおすすめします。
さて、「楽に残留リプルが求まる方法」とは以下のとおりです。整流直後の残留リプルは、「負荷抵抗(RL)」と「平滑コンデンサ容量」とでほとんど決定されてしまう、ということを利用します。この様子をまとめたのが図5です。横軸が負荷抵抗、縦軸が残留リプル、グラフ中の斜めの線がコンデンサ容量です。(注：このグラフは、本HomePageのオリジナルです。よそにはないですからね。)
図5 直流出力(Eo)に対する残留リプル(Er)含有率(%)表
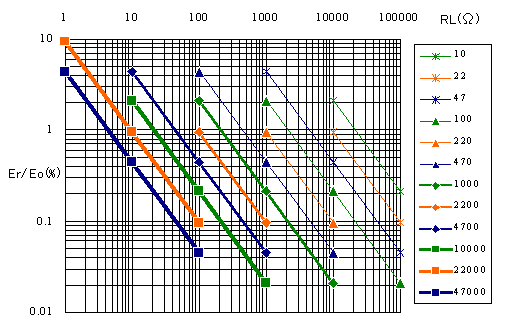両波整流（100-120Hz）の場合
横軸： RL（Ω）＝整流出力電圧 / 全直流電流
グラフ： C（μF）・・・コンデンサ容量
縦軸： Er/Eo（%）・・・直流出力（Eo）に対する残留リプル(Er)含有率(%)
「360V/120mA」のケース
たとえば、電源トランス「TANGO LH-150」の280Vタップを両波整流し、47μFで受けるようなコンデンサ・インプット回路に対して120mAの直流出力電流を取り出し、そのときの直流出力電圧が約360Vであるような場合の残留リプルを求めてみます。ところで、直流出力電圧の算出については、電源の設計その２ (実用の知識編)を参照してください。
負荷抵抗(RL) = 360V / 120mA = 3000Ω
平滑コンデンサ容量 = 47μF
ですから、グラフ上の「3000Ω」目盛と「47μF」の直線(細いブルー)との交点を見つけるとリプル含有率は「約1.5%」であることがわかります。つまり、直流出力電圧の約1.5%が残留リプルということになります。これを計算すると、
360V × 1.5%＝5.4V
になり、残留リプルは5.4Vと求まります。これは、実測値5.0V〜5.5Vとよく一致します。
「6.3V/1A」のケース
ところで、低圧大電流の場合でもこのグラフは使えるのでしょうか。では、6.3Vをブリッジ両波整流して、10000μFで受け、ここから6.3V、1Aのフィラメント電源を取り出した場合の残留リプルについてみてみましょう。
負荷抵抗（RL）＝6.3V / 1A＝6.3Ω
平滑コンデンサ容量＝10000μF
ですから、グラフ上の「6.3Ω」あたりの目盛と「10000μF」の直線（太いグリーン）を延長した交点を見つけるとリプル含有率は「約3%」になります。つまり、直流出力電圧の約3%が残留リプルということになります。これを計算すると、
6.3V × 3%＝189mV
になり、残留リプルは189mVと求まります。これも、実測値150mV〜170mVにかなり近い値です。図5のグラフは、高圧B電源でも、低圧ヒーター電源でも、広範囲にわたって通用します。
そして、整流直後の残留リプルさえわかれば、あとは前述したリプル・フィルターの計算によって、それぞれの電源における残留リプルがおおよそどれくらいになるそうなのか、簡単に求まるというわけです。
例題
以下のような回路における、各段の残留リプルを求めてみます。250V×2の電源を両波整流し、47μFのコンデンサ・インプットで受けます。以後、「200Ω・100μF」、「1kΩ・100μF」の2段リプル・フィルターが続きます。全直流電流は、100mA＋10mA＝110mAです。(図6)
図6
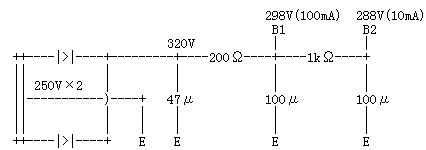
まず、整流出力電圧ですが、簡易計算(電源トランスの定格の80%〜90%の電流を取り出した時の一般値)ということで、250V × 1.28＝320Vが求まります。負荷(RL)は、320V / 110mA＝2.9kΩです。そこで、図5のグラフから、「2900Ω」目盛と「47μF」の直線（細いブルー）との交点を見つけると「約1.5%」が求まります。ですから、整流直後の残留リプルは、320V×1.5%＝4.8Vになります。(図7)
図7
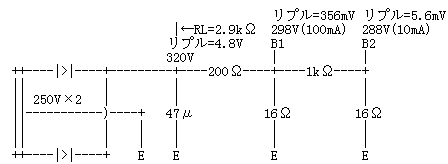
さて、「200Ω・100μF」、「1kΩ・100μF」のそれぞれのリプル・フィルターは、リプル周波数が100Hzだとして簡易計算で、「200Ω・16Ω」、「1kΩ・16Ω」と読み替えることができます。これはそれぞれ、16/(200+16)=0.0741倍、16/(1000+16)=0.0157倍の減衰率ですので、以後のリプル電圧は、4.8V×0.0741＝356mV、さらに、356mV×0.0157＝5.6mVが求められるわけです。(図7)
チョークの時の計算
抵抗とコンデンサで構成するリプル・フィルタは、設計が簡単で、しかも非常に安価です。しかし、抵抗による電圧降下の問題が、電源回路設計の足を引っ張ることもありえます。そんな時に有効なのが、チョークとコンデンサの組み合わせです。たとえば、TANGO製で「C-512」という比較的安価なチョークがあります。規格は、120mAを流した時のインダクタンスが5H、直流抵抗が100Ωです。5Hというと、100Hzでは3150Ω、50Hzでは1575Ωに相当します。計算方法は、
6.3 × 100Hz × 5H = 3150Ω
6.3 × 50Hz × 5H = 1575Ω
です。直流抵抗はわずか100Ωのままで、約3kΩ相当の抵抗を挿入したのと同等の効果が得られること、回路が単純であること等、嵩張って重いチョークですがなかなか捨てたものではありません。
半導体を使ったリプル・フィルタ回路
少ない電圧降下で、チョーク並あるいはそれ以上の効果が期待できるのが、半導体を使ったリプル・フィルタです。ここでは、トランジスタを使った基本回路とMOS-FETを使った基本回路について説明します。MOS-FETを使ったシンプルな回路
真空管式ミニワッターでは、MOS-FETを使って効果的にリプルを除去しています。基本回路は下図の通りです。MOS-FETのドレイン側に整流出力をつなぎ、ソース側が出口で80mAほど取り出しています。リプル電圧がピークで2〜3Vあるので、MOS-FETがこれを吸収するためにはドレイン〜ソース間には5〜6V程度の電圧の余裕が必要です。ゲート〜ソース間電圧が3Vあるのと56kΩと1.5MΩで分圧することで必要な電圧余裕を得ています。MOS-FETは、トランジスタのようなベース電流が流れないので、分圧の計算は簡単です。この回路は、電源をOFFにした時に47μFよりも100μFの方が先に放電します。その時にドレインとゲートの電圧が逆転します。それを防いでいるのが56kΩのところに入れたダイオードです。
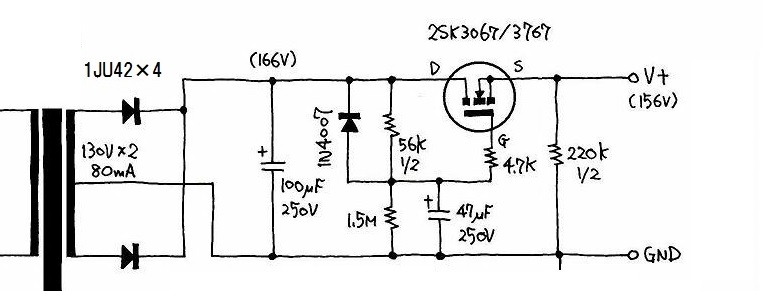図中の156Vは誤り。正しくは160V。
この回路は一種のソースフォロワと言えます。56kΩと47μFによってMOS-FETのゲートのところの残留リプルは1/1500以下に減っています。この回路の場合は1mVくらいです。そのためソース側の電源出力も1mVになります。電源インピーダンスは、MOS-FETのgmの逆数ですので2Ω〜5Ωぐらいです。非常に発振しやすいのでゲートに発振止めの抵抗を入れてあります。この抵抗値が大きいと高い周波数で電源インピーダンスが上昇します。20kHzで上昇させないためには3.3kΩ以下である必要があります。
ダーリントン・トランジスタを使ったシンプルな回路
下図（図8a）が、原回路です。耐圧が400V以上のパワートランジスタはhFEが非常に低く20〜30くらいしかありません。このままでは使えないので2個をダーリントン接続して大きなhFE得られるようにして使います。2SD798は、ダーリントン接続にした2個のトランジスタを1つのパッケージにしたものです。とても便利なトランジスタですが、入手は難しいでしょう。
トランジスタのコレクタ側からB+電源(300V)を供給し、エミッタ側から出力電流(100mA)を取り出します。トランジスタを動作させるためのベース電流は、抵抗(R1=39kΩ)によってコレクタ側から供給しますが、2SD798のhFEが「200」であるとすると、コレクタ電流約100mAのときのベース電流はコレクタ電流の1/hFE、すなわち1/200ですから、ベース電流は0.5mAです。抵抗(R1=39kΩ)による電圧降下は、1mA×39kΩ=19.5Vということになりベース電圧は、300V-19.5V=280.5Vとなります。2SD798のベース・エミッタ間電圧は約1Vなので、エミッタ電圧は279.5Vに落ちつきます。この回路は、一種のエミッタ・フォロワということができます。100mAを流した時の電源インピーダンスは約0.5Ωです。
そのとき、ベース側にコンデンサ(C)を挿入してベース電圧に含まれるリプルさえ除去してしまえば、コレクタ側にどんなにリプルが残っていても、エミッタ側(out)にはリプルは現われない、というしくみを使ってリプル・フィルタ効果をだそうというわけです。もし、トランジスタを使わずに、図1の抵抗とコンデンサだけのリプル・フィルタですと、100mAの電流が流れる場合で電圧降下を21Vでおさえようとすると、抵抗値は、20V/101mA=約200Ωにしかなりませんが、トランジスタを使うと抵抗値はなんと39kΩにもなり、同じコンデンサ容量であればほぼ200倍のフィルタ効果が期待できる(あるいはわずか1/200の容量のコンデンサで同じフィルタ効果が期待できる)ことになります。
しかし、この回路には重大な欠点があります。トランジスタのhFEのバラツキは異常に大きく、しかも温度変化等の外部要因に対してクリティカルです。そう簡単にベース電圧(※)が計算どおりの280Vに安定してくれません。
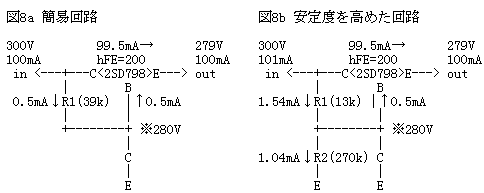
そこで、もうすこしベース電圧(※)の安定度を高めるようにちょっとだけ工夫したのが図8bの回路です。ベース〜アース間に抵抗(R2=270kΩ)を挿入して、ブリーダ電流(約1mA)を流すようにしています。ベース電流(0.5mA)とブリーダ電流(1mA)の比率が大きい程、ベース電圧(※)は安定しhFEの影響をうけにくくなります。しかし、ブリーダ電流が増えた分、抵抗(R1=13kΩ)の値が小さくなってしまいますから、フィルタ効果は減ってしまいます。それでも、トランジスタを使わない場合に比較すれば、図8bの回路でも65倍のフィルタ効果が期待できるのです。
半導体リプル・フィルタの注意点
半dd7導体リプル・フィルタを設計・製作する時の注意点はたくさんあります。（１）半導体の耐圧・・・250V以上の高圧に耐えるトランジスタはそんなに多くありません。MOS-FETなら高耐圧のものがたくさんありますので、MOS-FETをお勧めします。そして、いかなる場合も、短時間であっても、トランジスタ規格表上の「VCEO」を決して越えてはいけません。
（２）放熱とコレクタの絶縁・・・電力型のトランジスタのほとんどは、放熱板なしの状態ではほとんど電力を食わせることができません。そして、このようなトランジスタのほとんどが、胴体の金属部分(フランジ)がコレクタに接続されています。従って、いきなり放熱板やシャーシにねじ止めすると、コレクタがアースにショートしてしまいます。絶縁のための雲母板や樹脂フィルム、ビスの絶縁ワッシャが市販されていますが、シャーシの穴あけ時に残ったほんのわずかな「バリ」や「カエリ」が樹脂フィルムを貫通することによる絶縁破壊事故が絶えませんので注意してください。厚さ0.何ミリの間に250V〜400Vの高圧がかかっているのです。
（３）エミッタ/ソース側のショートと突入電流・・・半導体は、ちょっとした定格オーバーで簡単に、瞬間的に(音もなく)破壊します。特に注意したいのは、通電テスト時のエミッタ/ソース出力側のショート事故です。ドライバー等でうっかりエミッタ/ソース出力側とアース間を(瞬間でも)ショートさせると、トランジスタやMOS-FETに大電流が流れてたちまち昇天してしまいます。また、ショートさせていなくても、一見正常な回路でも同様の事故が起こります。
図9
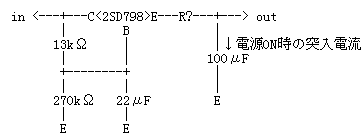
半導体リプル・フィルタの出力側に容量の大きなコンデンサ(100μF)があると、電源ON時に、このコンデンサを充電するための突入電流が半導体を襲います。こういった事故を防ぐためには、コンデンサを省略するか、保護抵抗(R?)を挿入します。一般的な真空管アンプのB電源では、保護抵抗(R?)の値は100Ωでは駄目な場合が多く、最低で150Ω、できれば200Ω欲しいところです。
（４）電流の逆流、電圧の逆転・・・図8bのようなブリーダ電流を流す設計を行った場合、電源OFFの後にトランジスタに電流の逆流現象が生じることがあります。電源OFF後数秒間は、真空管のヒーターがまだ暖まっているために回路には電流が流れていますが、やがて回路に流れる電流はゼロになってゆきます。そういう状況では、コンデンサに溜まっていた電荷の逃げ道が、トランジスタ・リプル・フィルタ回路の抵抗(図10では13kΩと270kΩ)だけしかない、ということもありうるわけです。
図10
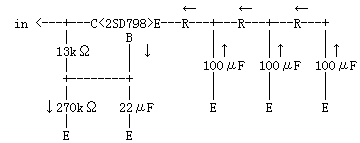
この場合、トランジスタのエミッタ〜ベース間にが逆電圧がかかり、電流も逆流します。この問題を回避するひとつの方法は、下流の方にも抵抗(※)を挿入して電荷の逃げ道を用意してやるというものです。もうひとつの方法は、ベース〜エミッタ間にダイオード(※)を入れてやって、逆流時のベース〜エミッタ間にバイパスを設けてやるというものです。(図11)
図11
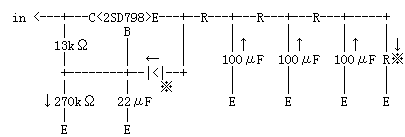
（５）遅延効果・・・半導体リプル・フィルタは、遅延効果という面白い副産物があります。フィルタ効果が大きければ大きいほど、電源ON時のフィルタ部分のコンデンサへの充電に時間がかかることになり、ベース/ゲート電圧(ひいてはエミッタ/ソース電圧)がゆっくりと上昇するようになるからです。しかし、13kΩと22μF程度の組み合わせでは遅延効果はほとんどありません。目に見えた効果が現われるのは、47kΩと100μF、10kΩと470μFくらいの組み合わせ以上です。
