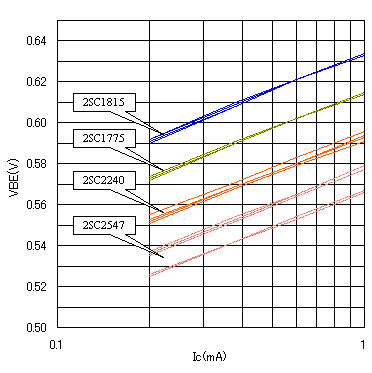
ベース〜エミッタ間電圧(VBE)とコレクタ電流(IC)の関係
本サイトの「私のデータ・ライブラリ」のページに「ローノイズ・トランジスタVBE実測データ」というデータがあり、左下図のグラフがあります。このグラフは、ベース〜エミッタ間電圧(VBE)とコレクタ電流(IC)の関係について、4種類のトランジスタを数本ずつ実測したものです。ベース〜エミッタ間電圧(VBE)が変化すると一定の比率でコレクタ電流(IC)が変化している様子がわかります。トランジスタの型番やメーカーが異なっても、どれも同じ角度を持った特性になっていますね。実は、この角度こそがトランジスタの基本的特性の正体で、これを解析すればトランジスタ回路の利得がすべて説明できるというちょっと面白いデータなのです。
左上のデータを取った2SC1815のうちの1本について、コレクタ電流=0.1mA〜10mAの範囲でVBEとの関係を精密に測定したのが右上のグラフです。
グラフ中からIc=0.2mA、1mA、5mAの3つのポイントを選び、このポイントを基点としてVBEが±0.01Vとなる範囲にマーキングしました。たとえば、中央のケースではIC=1mAの時は、VBE=0.63Vですが、VBE=0.62になるとIc=0.7mAとなり、VBE=0.64になるとIc=1.47mAとなります。つまり、VBEに±0.01Vすなわち0.02Vの変化を与えると、IC=0.7〜1.47mAとなって0.77mAの変化が得られたわけです。同様にして、IC=0.2mAとIC=5mAの場合も求めて表にしてみました。
コレクタ電流(IC) 0.2mA 1mA 5mA ベース〜エミッタ間電圧(VBE)の変化 ±0.01V コレクタ電流(IC)の変化 0.153mA
(0.137〜0.29mA)0.77mA
(0.7〜1.47mA)3.82mA
(3.38〜7.2mA)このデータから、ベース〜エミッタ間電圧に同じ0.02Vの変化を与えていても、コレクタ電流が少ないとコレクタ電流の変化は小さくなり、コレクタ電流が多いとコレクタ電流の変化も大きくなることがわかります。どうやら、設定したコレクタ電流の大きさによって利得が変化するようです。
トランジスタをgmでとらえる
コレクタ電流が1mAの場合について考えてみます。ベース〜エミッタ間電圧に0.02Vの変化をインプットしたら0.77mAのコレクタ電流の変化がアウトプットとして得られたというのは、真空管でいうところのグリッド入力とプレート電流の関係と同じですね。
0.02Vの変化をインプット → アウトプットとして0.77mAの変化・・・IC=0.2mAの時真空管ではこの関係のことを相互コンダウタンス(gm)と言い表しましたが、トランジスタでも全く同じように考えてこの関係をgmとしてとらえます。この時のgmは、
0.02Vの変化をインプット → アウトプットとして0.153mAの変化・・・IC=1mAの時
0.02Vの変化をインプット → アウトプットとして3.82mAの変化・・・IC=5mAの時gm=0.153mA÷0.02V=7.57mS・・・IC=0.2mAの時となります。「mS」はミリ・シーメンスと読み、電圧の変化によって電流がどれくらい変化するかを表した単位です。1S(シーメンス)は、1Vの電圧変化に対して1Aの電流変化が生じるという意味で、1mS(ミリ・シーメンス)は、1Vの電圧変化に対して1mAに電流変化が生じるということを表しています。38.5mSは、1Vの電圧変化に対して38.5mAの電流変化、0.01Vでは0.385mAの電流変化なわけです。
gm=0.77mA÷0.02V=38.5mS・・・IC=1mAの時
gm=3.82mA÷0.02V=191mS・・・IC=5mAの時上記の3つの結果の関係に注目してみます。ICが5倍になるごとにgmも5倍になっています。トランジスタのgm値はICに比例するのです。
7.57mS〜(×5倍)〜38.5mS〜(×5倍)〜191mSさて、gm=38.5mSの増幅素子を使って増幅回路を組んだ場合、負荷インピーダンスと利得の関係は以下のようにして求めるのでしたね。
利得=負荷インピーダンス(kΩ)×gm(mS)そこで、負荷インピーダンスが100Ωの時、1kΩの時、10kΩの時、12kΩの時、22kΩの時を求めると上の表の利得(3.85〜847倍)になるわけです。
ベース電流はどうなっているか
このように、真空管とトランジスタはともに、電圧の変化を入力すると電流変化としてアウトプットが得られるという点で同じように考えることができます。この作用において真空管とトランジスタの最も重要な違いは、真空管においてはグリッドには電流が流れないと考えて設計してかまわないのに対して、トランジスタではベースには無視でないくらい大きな電流が流れることを考慮しなければならないということです。ところで、「利得と入力インピーダンスの計算法」のページで、入力インピーダンスは以下の式で求められるということを書きました。
入力インピーダンス = hFE × { RE + ( 26Ω ÷ IC ) }そして、hFEが240のトランジスタを使い、コレクタ電流が1mAで、エミッタ抵抗がない(0Ω)の回路の入力インピーダンスは、
入力インピーダンス = 240 × { 0Ω + ( 26Ω ÷ 1mA ) } = 6.24kΩになるのでしたね。この回路の入力に±0.01Vの信号を入力したわけですから、そこには
±0.01V ÷ 6.24kΩ = ±0.0016mA(1.6μA)の電流が流れていることになります。この電流はベース電流になります。ベース電流が±1.6μAの変化をしたわけですから、コレクタ電流は240倍されて±0.384mAの変化になるわけです。トランジスタの場合は、「ベース〜エミッタ間電圧の変化→コレクタ電流の変化」ととらえることもできるし、「ベース電流の変化→コレクタ電流の変化」ととらえることもでき、いずれの考え方であっても結果は同じになります。そこが真空管と決定的に違います。ところが、「ベース電流の変化→コレクタ電流の変化」ととらえた場合、そのベース電流はhFEが大きいほど小さくて済むわけですが、hFEが大きいほど電流の増幅率は大きくなるので、結局hFEはアンプの利得には関係ない、ということになって計算が無駄になります。ですから「ベース〜エミッタ間電圧の変化→コレクタ電流の変化」ととらえた方が合理的なのです。以下の利得の計算式に、
利得 = RC ÷ { RE + ( 26Ω ÷ IC ) }hFEが出てこないのはそういう理由があるからです。
ところで、38.5mSは0.0385Sです。0.0385Sという値と26Ωという値の関係に気付いた方はいらっしゃいますか?これは互いに逆数なんです。つまり同じものというわけ。
1÷0.0385S=26Ωこれですべての回路動作の関係が出揃いました。これが「その3トランジスタ増幅回路の基礎」のページの「ベース電流値・・・その大きさは±1.6μA(=0.0016mA)」の理由です。
そういうことでいいの?
上のデータを見ると、たとえばコレクタ電流=1mAの場合、ベース〜エミッタ間電圧が0.01V高くなった時のコレクタ電流は0.47mA増しなのに、0.01V低くなった時のコレクタ電流は0.3mA減だからプラス側とマイナス側でバランスが合わないじゃないの、これでいいの、と言いたくなると思います。そう、これでいいんです。事実、±0.01Vが入力された場合のコレクタ側の出力波形は上下がいびつでかなり歪んでいます。しかし、音を聞いてみると歪んだ感じはほとんどなくてかなりまともです。そもそも、トランジスタの素の増幅特性なんてそんなもんなんです。真空管はすこしましなものもありますが、大体似たようなものです。
これは±0.01Vだからこんなに不揃いなわけで、±0.001Vになると不揃いな度合いは1/10になります。±0.0001Vになると1/100になります。増幅素子の非直線性による歪みの大きさは信号の大きさに比例する性質があり、微小信号になればなるほど非直線性は無視できるようになるのです。ここではイメージをつかみやすくするために±0.01Vを使っただけです。あとは、どのように工夫してこの不完全な直線性を完全なものに近づけるか、回路方式で工夫することになります。
トランジスタが普及しはじめた頃、真空管派とトランジスタ派の間でさまざまな論争がありました。そのなかのひとつに「真空管はすっぴんのままでも優れた直線性を示すが、トランジスタはひどい直線性で見られたものではない!」という主張があります。実際に両方の素子を使って設計してみると、半分は当たっているように思います。面白いことに、真空管を使った場合は容易に1%以下の歪み率特性が得られるのに、0.01%を割ることは非常に難しい(というよりほとんど不可能)のに対して、トランジスタを使った場合は差動回路や負帰還など回路技術に助けてもらわないと歪み率特性で真空管に負けてしまうのに、ちょっと工夫するだけで容易に0.01%以下の歪み率特性が得られてしまうということです。
但し、低歪み率を追いかけただけでは音の良いアンプはできない、という別の壁があり、何故だかわかりませんが真空管はこれを簡単に超えてしまうのに、トランジスタはなかなか超えられずにいる、ということもひとつの事実です。